Classification Algorithms

Classification algorithms are generally grouped into supervised and unsupervised methods, although some algorithms combine features from each group. In the supervised case, a specialist identifies terrain classes in a scene, and class means and/or boundaries are identified in parameter space that serve to separate the classes. This is called "training", and the training data can be chosen from the scene itself, or from previously acquired scenes that possess similar characteristics. After the training, the algorithm automatically assigns classes to each pixel based on the predetermined class means or boundaries.

In a basic unsupervised classifier, the algorithm has no prior information of the scene content or of the terrain classes present. The algorithm examines the parameter space for each scene, and assigns classes and boundaries based on the clustering of pixels. Sometimes, the classes and boundaries can be based upon physical models. In either case, the operator must identify each class manually after the class assignments.

The supervised classifiers have the disadvantage of requiring operator input, and the classes obtained tend to be scene specific. The unsupervised classifiers sometimes yield classes whose physical meaning is uncertain. In the next few subsections, an example of an unsupervised and a supervised classifier are given, which have been applied to polarimetric radar data. Finally, a promising new classifier is outlined, which combines the best features of the two previous types.

Unsupervised Classification Based on H/A/α Parameters

In any classifier, the choice of parameters is important, and in the case of polarimetric radar data, content-independent scattering models can be used to get parameters that provide reasonable class separation. A current example is the H / A / set of parameters derived from an eigenvalue decomposition of the coherency matrix. The H / A / algorithm was developed by Cloude and Pottier, who showed that terrain classes sometimes produced distinct clustering in the H / plane .

The H / plane is drawn in Figure 7-1. The observable alpha values for a given entropy are bounded between curves I and II (i.e. the shaded areas are not valid). This because the averaging of the different scattering mechanisms (i.e. averaging of the different eigenvectors) restricts the range of the possible a values as the entropy increases. As H and are both invariant to the type of polarization basis used, the H / plane provides a useful representation of the information in the coherency matrix .

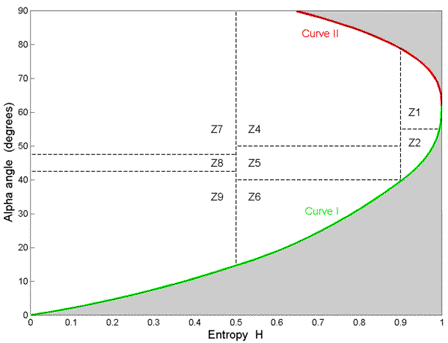
Figure 7-1: The H / 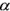plane showing the model-based classes and their partitioning. A description of the classes (Z1 - Z9) is given in the text.

The bounds shown in Figure 7-1 (Curve I and Curve II) show that when the entropy is high, the ability to classify different scattering mechanisms is very limited. An initial partition into nine classes (eight usable) has been suggested by Cloude and Pottier , and is shown in Figure 7-1. Classes are chosen based on general properties of the scattering mechanism and do not depend up on a particular data set. This allows an unsupervised classification based on physical properties of the signal. The class interpretations suggested by Cloude and Pottier are as follows (see for more details):

• Class Z1: Double bounce scattering in a high entropy environment
• Class Z2: Multiple scattering in a high entropy environment (e.g. forest canopy)
• Class Z3: Surface scattering in a high entropy environment (not a feasible region in H / space)
• Class Z4: Medium entropy multiple scattering
• Class Z5: Medium entropy vegetation (dipole) scattering
• Class Z6: Medium entropy surface scattering
• Class Z7: Low entropy multiple scattering (double or even bounce scattering)
• Class Z8: Low entropy dipole scattering (strongly correlated mechanisms with a large imbalance in amplitude between HH and VV)
• Class Z9: Low entropy surface scattering (e.g. Bragg scatter and rough surfaces)

It is important to note, however, that the boundaries are somewhat arbitrary and do depend upon the radar calibration, the measurement noise floor and the variance of the parameter estimates. Nevertheless, this classification method is linked to physical scattering properties, making it independent of training data sets. The number of classes needed as well as the usability of the method depends upon the application. Additional interpretation of the classes is given in , where a small change in the class boundaries is proposed.

The third variable of polarimetric anisotropy has been used to distinguish different types of surface scattering. The H / A-plane representation for surface scattering is given in Figure 7-2, where the shaded region is not feasible. The line delineating the feasible region can be calculated using a diagonal coherency matrix with small minor eigenvalues 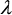₂ and 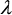₃, with 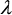₃ varying from 0 to 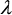₂.

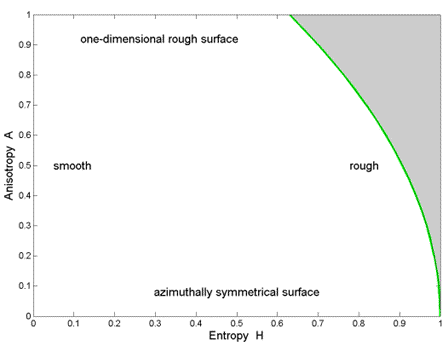
Figure 7-2 Types of surface scattering in the Entropy/Anisotropy plane.

Introduction of the anisotropy to the feature set represents a third parameter that can be used in the classification. One approach is to simply divide the space into two H / planes using the green plane shown in the 3-D space of Figure 7-3, one side for A 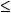0.5 the other side for A > 0.5. This introduces 16 classes if the H / planes are divided according to Figure 7-1. Note that the upper limit of H is restricted when A > 0, as shown in Figure 7-2.

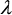The H / A / -classification space, given in Figure 7-3, now provides additional ability to distinguish between different scattering mechanisms. For example, high entropy and low anisotropy (₂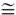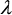₃) correspond to random scattering whereas high entropy and high anisotropy (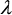₂ >> 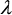₃) indicate the existence of two scattering mechanisms with equal probability.

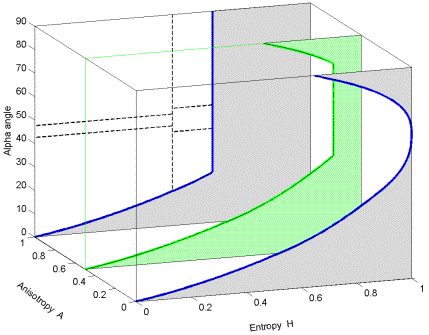
Figure 7-3: Illustration of how an A = 0.5 plane (green) creates 16 classes from the original 8 H / classes shown in Figure 7-1. This gives 16 regions in the Entropy / Anisotropy / space for use in an unsupervised classifier.

The three parameters H, A and are based on eigenvectors and eigenvalues of a local estimate for the 3x3 Hermitian coherency matrix ("Hermitian" means a square matrix that has conjugate symmetry - it has real eigenvalues). The basis invariance of the target decomposition makes these three parameters roll invariant, i.e. the parameters are independent of rotation of the target about the radar line of sight. It also means that the parameters can be computed independent of the polarization basis.

Estimation of the three parameters H, A and allows a classification of the scene according to the type of scattering process within the sample (H, A) and the corresponding physical scattering mechanism (). The data need to be averaged in order to allow an estimation of H, A and (without averaging, the coherency matrix has rank 1), which has the benefit of reducing speckle noise .

An example of the clustering of pixels from a sea ice SIR-C scene is shown in Figure 7-4a . The H/A plane shows evidence of clustering into two and possibly three classes. Figure 7-4b shows the distribution of H/ values for a white spruce field; the target shows a dominant dipole scattering ( about 45°), with a high value of entropy H of about 0.8, indicating rather heterogeneous scattering. Figure 7-4b was produced on CCRS's Polarimetric Workstation (PWS).

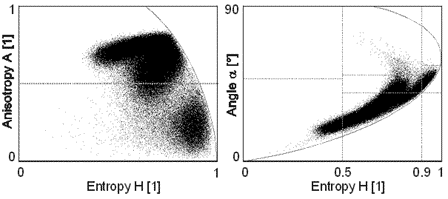
Figure 7-4a Scatter plots showing distribution of SIR-C ice data over the H / A / classification space (Scheuchl)

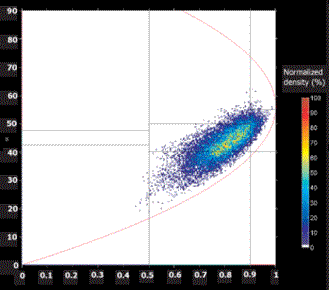
Figure 7-4b Scatter plots showing distribution of SIR-C ice data over the H / A / classification space.

Supervised Bayes Maximum Likelihood Classification

An alternative to the model-based approach is to define classes from the statistics of the image itself. The classes are defined by an operator, who chooses representative areas of the scene to define the mean values of parameters for each recognizable class (hence it is a "supervised" method). A probabilistic approach is useful when there is a fair amount of randomness under which the data are generated. Knowledge of the data statistics (i.e. the theoretical statistical distribution) allows the use of the Bayes maximum likelihood classification approach that is optimal in the sense that, on average, its use yields the lowest probability of misclassification .

After the class statistics are defined, the image samples are classified according to their distance to the class means. Each sample is assigned to the class to which it has the minimum distance. The distance itself is scaled according to the Bayes maximum likelihood rule.

Bayes classification for polarimetric SAR data was first presented in 1988 . The authors showed that the use of the full polarimetric data set gives optimum classification results. The algorithm was only developed for single-look polarimetric data, though. For most applications in radar remote sensing, multi-looking is applied to the data to reduce the effects of speckle noise. The number of looks is an important parameter for the development of a probabilistic model.

The full polarimetric information content is available in the scattering matrix S, the covariance matrix C, as well as the coherency matrix T. It has been shown that T and C are both distributed according to the complex Wishart distribution . The probability density function (pdf) of the averaged samples of T for a given number of looks, n, is

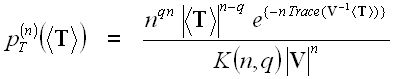(7.1)

where:

• <T> is the sample average of the coherency matrix over n looks,
• q represents the dimensionality of the data (3 for reciprocal case, else 4),
• Trace is the sum of the elements along the diagonal of a matrix,
• V is the expected value of the averaged coherency matrix, E{<T>}, and
• K(n,q) is a normalization factor.

To set up the classifier statistics, the mean value of the coherency matrix for each class V_m must be computed

(7.2)

where _m is the set of pixels belonging to class m in the training set.

According to Bayes maximum likelihood classification a distance measure, d, can be derived :

(7.3)

where the last term takes the a priori probabilities P(_m) into account. Increasing the number of looks, n, decreases the contribution of the a priori probability. Also, if no information on the class probabilities is available for a given scene, the a priori probability can be assumed to be equal for all classes. An appropriate distance measure can then be written as :

(7.4)

which leads to a look-independent minimum distance classifier:

(7.5)

Applying this rule, a sample in the image is assigned to a certain class if the distance between the parameter values at this sample and the class mean is minimum. The look-independence of this scheme allows its application to multi-looked as well as speckle-filtered data . This classification scheme can also be generalized for multi-frequency fully polarimetric data provided that the frequencies are sufficiently separated to ensure statistical independence between frequency bands .

The classification depends on a training set and must therefore be applied under supervision. It is not based on the physics of the scattering mechanisms, which might well be considered a disadvantage of the scheme. However, it does utilize the full polarimetric information and allows a look-independent image classification.

Note that the covariance matrix can also be used for this type of Bayes classification. The coherency matrix was chosen for the simple reason of compliance with the H / A / -classifier described in the previous section.

A Combined Classification Algorithm

Both unsupervised and supervised methods described above have their weaknesses. For the H / A /  -classification, the thresholds are somewhat arbitrary and not the entire polarimetric information can be used due to the inability to determine all four angles that parameterize the eigenvalues. The Bayes minimum relies on a training set or initial clustering of the data. However, each algorithm overcomes some of the shortcomings of the other.

Therefore, a combination of the two algorithms seems attractive . An improved classification can be obtained by first applying the H / A /  unsupervised classifier to set up and cluster 16 initial classes, followed by the minimum distance classifier based upon the distribution of clustered parameters. The distribution can be taken from the complex Wishart distribution, and iterations can be used to optimize the class separation boundaries , , .

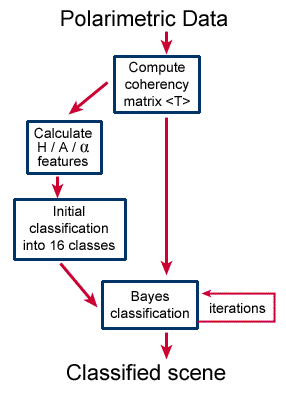
Figure 7-5: Combined Entropy / Anisotropy /  - minimum distance classifier

The combined algorithm is outlined in Figure 7-5. It can be viewed as an unsupervised algorithm, as the initial classification is unsupervised. However, as the iterations refine the cluster means and boundaries, the final classes should be scrutinized and assigned labels based upon a physical interpretation. Note that while the initial clustering is made in the H / A /  domain, the minimum distance classification is performed using the coherency matrix directly. After the Bayes classification, the clusters may overlap in the H / A /  domain. The classifier results do depend upon the number and diversity of classes input to the Bayes classifier, so it is always useful to experiment with different initial classes.

An example of the results of the combined H / A/  Bayes classification algorithm is given in Figure 7-6. Four sea ice types, three water classes and four land classes have been extracted from an April 1994 SIR-C image off the west coast of newfoundland . The level of detail of the extracted ice types is an indication of the power of computer classification of polarimetric radar data.

Classification algorithms can include a segmentation algorithm in which neighbouring pixels that have common characteristics are grouped together prior to the assignment of classes. If done properly, segmentation can significantly improve the classification results .

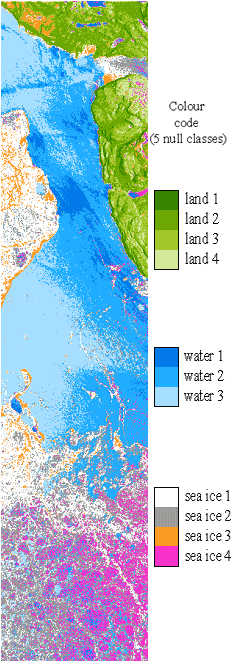
Figure 7-6: Classification of land, ocean and ice types from a SIR-C polarimetric C-band scene off the West coast of newfoundland .