Basics of SAR Polarimetry
Introduction to EM waves and their properties
An electromagnetic (EM) plane wave has time-varying Electric and Magnetic Field components in a plane perpendicular to the direction of travel![]() . The two fields are orthogonal to one another, and are described by Maxwell's equations
. The two fields are orthogonal to one another, and are described by Maxwell's equations ![]() . The fields propagate at the speed of light in "free space", which includes most realistic atmospheric conditions. Three parameters are necessary and sufficient to describe the propagation of EM waves in a given medium: dielectric constant (or permittivity), permeability and conductivity.
. The fields propagate at the speed of light in "free space", which includes most realistic atmospheric conditions. Three parameters are necessary and sufficient to describe the propagation of EM waves in a given medium: dielectric constant (or permittivity), permeability and conductivity.
In general, when an EM wave is emitted from a source, such as a radar antenna, it propagates in all available directions, (with a specific field strength and phase in each direction). At a long distance from the antenna, we can assume that the wavefront lies on a plane, rather than on the surface of a sphere. Since we are only interested in what happens to the wave along one specific direction, the "plane wave" assumption is appropriate.
 Did you Know?
Did you Know?
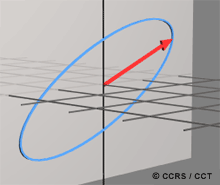
The predictable component of the EM wave has a characteristic geometric structure, which defines its polarization properties. When viewed along its direction of propagation, and assuming horizontal and vertical axes with respect to a specific coordinate system (e.g. axes defined parallel to the long and short sides of the radar antenna), the tip of the Electric Field vector traces out a regular pattern. The length of the vector represents the amplitude of the wave, and the rotation rate of the vector represents the frequency of the wave. Polarization refers to the orientation and shape of the pattern traced by the tip of the vector, as discussed in the next section.
Polarization is an important property of a plane EM wave. Polarization refers to the alignment and regularity of the Electric and Magnetic Field components of the wave, in a plane perpendicular to the direction of propagation. By convention, we direct our attention to the Electric Field component of the wave, as the orthogonal Magnetic Field component "follows" it according to Maxwell's equations (the Magnetic Field is directly related to the Electric Field, and can always be calculated from it). For this reason, the EM wave can be characterized by the behaviour of the Electric Field vector as a function of time. The propagation of an electromagnetic wave is illustrated in Figure 1-1.
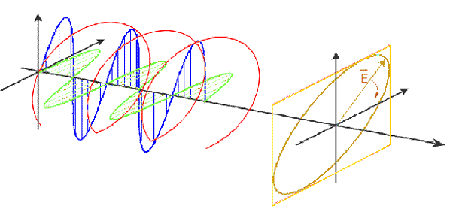
The waveform of the Electric Field vector can be predictable or random, or a combination of both. A random component is like pure noise, with neither a recognizable frequency nor a pattern to its amplitude. An example of a predictable component is a monochromatic sine wave, with a constant, single frequency and a constant amplitude. An EM wave that has no random component is called fully polarized.
Page details
- Date modified: