Managing Energy Storage Capacities Dispersed in an Electrical Grid to Reduce the Effects of Renewable Energy Source Variability
Lead Proponent: La Corporation de l’École Polytechnique de Montréal
Location Montreal, QC
ecoEII Contribution: $ 1,109,000
Project Total: $ 1,531,000
Project Background
The “smart grid” concept involves the use of information technologies in order to support power grid operation. Power grid operators responsible for electricity transmission or distribution must adapt their practices and tools in order to manage a grid with greater variable renewable energy and to support the future integration of electric vehicles in Canada. The use of energy storage is being considered to mitigate renewable energy source variability on the power grid. In a large-scale distributed energy storage system, the presence of an enormous number of control points poses a significant challenge to grid operators. Recognizing the technology gap, École Polytechnique de Montréal proposed the project “Managing Energy Storage Capacities Dispersed in an Electrical Grid to Reduce the Effects of Renewable Energy Source Variability” for eceoEII funding. The project was awarded $1,109K to apply an optimizing technique to the complex control problem for large-scale distributed energy storage unit management in power grids.
Results
The proponent renamed the Project “smartDESC” or smart Distribution Energy Storage Controller. The objective was to provide an approach to control that could be applied to millions of energy storage sites in an electrical grid, such as water heaters, space heaters, electric vehicle batteries, and so on. The approach taken was based on mean field control theory, which takes advantage of the predictability associated with the aggregate behaviour of a large number of homogeneous items that have to be controlled (e.g., millions of water heaters) so that ultimate control is as local as possible, requiring that only a minimum of information be exchanged between the local level and a more general level that compiles statistics about the group and transmits the desired collective behaviour to local controllers, such as a mean energy level for the population, as well as the desired progression of that level over the coming hours.
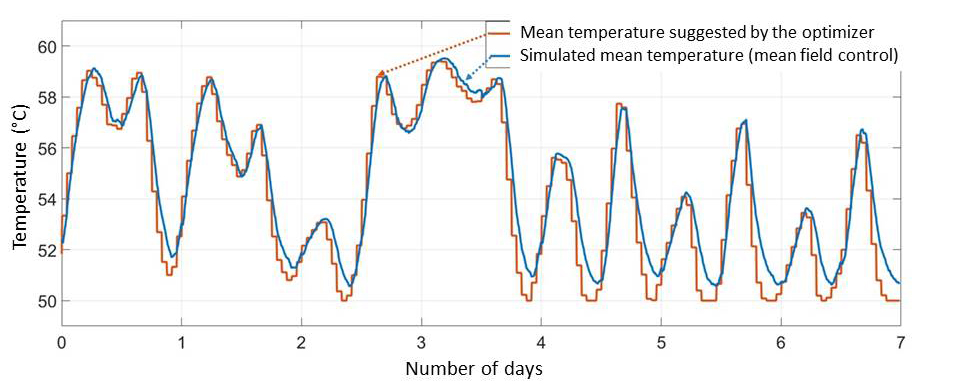
Figure 1: Changes in the mean temperature of the water heater population with mean field control over 400 houses
Depicts the outcome of the simulation in terms of water heater temperature. The red line is the target mean temperature calculated by the optimizer, and the blue is the simulated mean temperature for the population of 400 houses all fitted with a mean field controller. A point is depicted every five minutes along each curve.
This figure illustrates the mean field controllers’ excellent ability to follow the mean temperature target when the mean temperature follows an increasing trajectory (“loading” period of the water heater fleet). However, the two curves uncouple when the target mean temperature drops below 52°C. This uncoupling can be explained by two factors:
- The central optimizer always considers a normal distribution of the water heater population around the mean temperature. However, this approximation is valid only in the domain [52, 58]°C. Near the 50 and 60°C limits, the local controller (mean field or not) does not allow the temperature to rise above 60°C or drop below 50°C for customer safety and comfort reasons, resulting in a distortion of the presumed normal distribution, which then crashes at these limits, thereby biasing the optimizer’s projections.
- The water heaters’ heating and cooling mechanisms are not the same. During heating, power is injected into the water heater, which is always possible. Conversely, cooling requires customers to draw hot water, which is a stochastic process. The controller can therefore do nothing to accelerate the unloading of the water heaters if its pace is slower than the optimizer projected.
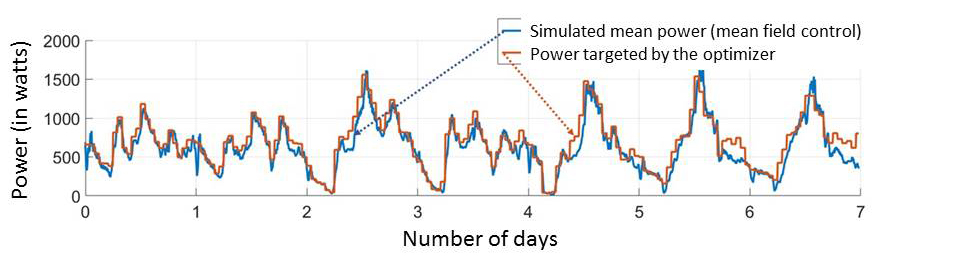
Figure 2: Mean power consumed by the water heater population with mean field control over 400 houses
Depicts the mean power consumed by the water heater population when the population is subject to the mean field control. It is interesting to consider this figure alongside Figure 1. Of particular note is the close proximity of the optimal power (red) and simulated power (blue) curves, which shows that the local control does its job very well. It is important to remember that this controller receives no power set point, but only the trajectory of the mean temperature of the water heater population.
Notice, though, that a few instances of uncoupling, for example at the end of the fifth day, are related to the gap between the desired mean temperatures and the mean temperatures achieved by the control (effect of the limits, as discussed above). Some solutions are currently being explored to improve the control and/or optimization when a significant proportion of the population reaches the temperature limits. The next section provides more detail about the temperature distribution within the water heater population.
All of the components needed to complete a simulated proof of concept for the mean field control of a population of water heaters installed in an electrical distribution network were developed as part of this project. This primarily entailed developing models of storage devices (e.g., water heaters) and telecommunications networks (mesh network of smart meters). Mathematical developments were also required in terms of the control algorithms themselves, as well as to optimize the overall collective behaviour of the storage elements based on a specific objective, e.g., flattening the electricity consumption curve, maximizing wind penetration, etc. All of these developments ultimately took the form of computer codes in various environments and languages (Java, C++, Fortran, etc.). An overall simulator had to be developed, based on the JADE multi-agent platform, to ensure the interoperability of all of these codes in a common computational space. Finally, a physical platform with a real water heater controlled by a mean field controller was built. The platform made it possible to confirm that the thermal model of the water heater used in the simulator was reliable. It was also possible to confirm that the local controller required for the mean field control was physically feasible without having to use sophisticated components: a simple microcontroller, some Ethernet or WiFi telecommunications equipment and basic instruments are sufficient.
This project also showed that the mean field control resolves the peak problem created by load recovery in electrical grids, i.e., a power peak that occurs after the electricity supply is restored to a grid following a disruption. The mean field control also requires very little bandwidth in terms of telecommunications. As a result, a mean field control applied to an electrical grid could make do with communication via a network of very low-flow smart meters and would take up less than 1% of their bandwidth.
Benefits to Canada
Advancements in the methods used to control distributed energy storage reduces the need for spinning energy reserves, enables more efficient operation of energy generation units, and facilitates the integration of renewable energy sources and electric vehicles into the grid. This will help to reduce greenhouse gas emissions in Canada.
Next Steps
At this stage, the concept could be implemented almost as-is in a pilot project, provided that the following are found: a manufacturer to produce the mean field controllers; an electricity distributor to install the necessary equipment; an aggregation service provider to manage data; and a proponent to oversee project management and coordination. Technology transfer from École Polytechnique to industry would be required.
Page details
- Date modified: