Polarimetric data expressed in the power domain
There are many different ways of representing the scattering properties of a target, and they are often expressed in the power domain. Several of the most widely used power representations are introduced in this section.
- The Covariance and Coherency Matrices
- Averaging the power forms
- Data compression and storage formats
- The Stokes and Mueller matrices
The Covariance and Coherency Matrices
The scattering vector or covariance vector kC is a vectorized version of the scattering matrix. Assuming reciprocity, whereby Svh = Shv , this vector is
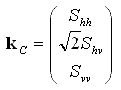(2-1)
It is convenient to construct a power-domain representation of the scattering properties, which is done by forming the product of this vector with itself. This results in the covariance matrix, which also fully describes the scattering properties of the target target [
, Section 5-4.10]:
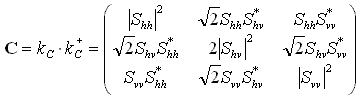(2-2)
where + denotes conjugate transpose and * the conjugate. The covariance matrix has conjugate symmetry.
The coherency matrix is closely related to the covariance matrix, and is preferred by some analysts . To obtain the coherency matrix, the scattering matrix is vectorized in a different way using the Pauli spin elements (again assuming reciprocity):
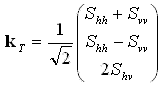(2-3)
This vector is sometimes preferred because its elements have a physical interpretation (odd-bounce, even-bounce, diffuse, etc.). Note that some authors use (Svv - Shh) for the second element of this vector , obtaining an equivalent analysis. Again, the information in (2-3) is expressed in the power domain by forming the "product" of this vector with itself, resulting in the coherency matrix:
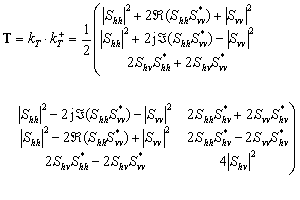(2-4)
The eigenvalues of the covariance matrix and the coherency matrix are real and are the same. The sum of the diagonal elements (the trace) of both matrices is also the same, and represents the total power of the scattered wave if the incident wave has unit power. Note that most authors use the BSA convention for these definitions.
Averaging the power forms
Averaging of adjacent samples is very useful in polarimetric radar data analysis. It has a similar effect as look summation in single-polarization SAR processing. It reduces the "noisy" effects of speckle, but at the expense of degrading the resolution of the image , . When values in the neighbourhood of a sample are averaged, scatterers that were once represented by distinct samples become consolidated in the image.
Did you Know?
When the scattering matrix of a single pixel is measured by the radar system, there are not enough degrees of freedom to represent noise as well as the target's scattering properties, even though noise is present in the observation. For this reason, a single scatterer is assumed even though there may be multiple scattering mechanisms and noise present in the pixel. However, when converted to a power representation and neighbouring samples are averaged, a composite pixel is obtained in which the noise and different scattering mechanisms can be explicitly represented.
The resulting reduction of speckle and noise, and the grouping of scatterers, makes the image easier to interpret and can make automatic classifiers work more reliably .
Averaging is performed in the power domain, because the energy of individual components is preserved in power representations (energy is not preserved when averaging in the "voltage" domain). Usually the Stokes, covariance or coherency matrix representations are used for the averaging. The averaging is usually performed as a post-processing operation, by averaging the power matrix values of adjacent samples. Averaging has the additional advantages of reducing the data volume, and can be used to create equal pixel spacing in ground range and in azimuth.
Data compression and storage formats
In order to deal efficiently with data from the AIRSAR and SIR-C polarimetric radars, scientists at the Jet Propulsion Lab (JPL) sought a way of storing and distributing the data that was simple, compact and contained all the essential information for data interpretation and classification. Rather than storing the four complex elements of the scattering matrix, possibly using 32 bytes per pixel, they chose the Stokes
Did you Know?
Did you know that the Stokes and covariance matrices contain phase information, even though they are power representations? This is because the cross terms such as the expected value of (Ehh Evv*) are complex numbers, and the angle of the complex number depends upon the phase angle between the HH and VV channels.
(Kennaugh) matrix for the AIRSAR data, and compressed each sample (or group of averaged samples) into a 10-byte word. Other radar systems have used the covariance matrix for data compression , page 292.
In the JPL scheme, the total power of each sample is computed and stored in 2 bytes, one for the mantissa and one for the exponent. The remaining 8 unique elements of the Stokes matrix are normalized by the top left element, M11, and stored in 1 byte each. The four smallest of these, related to the cross-products of the co-pol and cross-pol channels, are square rooted as well. The original elements of the Stokes matrix are easily recovered from the stored values .
With higher storage capacities becoming available, it is possible to store the full scattering (Sinclair) matrix for each sample, without averaging to reduce the data volume. More sophisticated methods of compressing radar image data have been developed for single channel data, e.g. based upon the DCT or wavelets, but these methods have not been fully tested on polarimetric data yet.
Whiz quiz
Question 1: What is meant by a "scattering mechanism"? The answer is...
Question 2: How is a "scattering mechanism" defined? The answer is...
Question 3: Why is the covariance matrix considered to be a "power" representation? The answer is...
Whiz quiz - answer
Answer to question 1: Every feature or structure on the ground scatters radar energy in a certain way. Examples are water, a cornfield, a farmhouse, or a car. Most of these features scatter energy in a different way from the others. The term "scattering mechanism" is an attempt to characterize the scattering from a given feature in terms of simple elements for which we know or can model the scattering behaviour. Examples of scattering mechanisms are a sphere, a dihedral, a helix, and composite scatterers such as a random distribution of dipoles.
Answer to question 2: There are two basic ways of defining a "scattering mechanism". The first is to create a physical model of a scatterer, such as a dipole or a trihedral corner reflector. Then mathematical and physical principles (such as Maxwell's equations) are used to derive how the EM waves scatter off the surface. The scattering is then expressed as a scattering matrix, or its derivatives such as the Stokes or covariance matrix. The term "mechanism" refers to the elemental scatterer or model, plus its associated mathematical definition of scattering behaviour.
The second method is to make an explicit measurement of the scattering, either in the field or under laboratory conditions (e.g. in an anechoic chamber). In this case, the measured echo is usually made up of a number of elemental mechanisms, and mathematical procedures have been developed to separate the signal into its constituent components (e.g. eigenvalue decomposition of the coherency matrix). Each component is then referred to as a scattering mechanism, and hopefully can be related to a physical model mentioned in the previous paragraph.
Answer to question 3: Because the scattering matrix elements relate the "voltage" of the scattered EM wave (the Electric Field strength) to the "voltage" of the incident wave, and the covariance matrix is formed from "products" of these elements. In other words, the covariance matrix relates the power of the scattered EM wave to the power of the incident wave.
The Stokes and Mueller matrices
When the polarization of the incident wave is described by a Stokes vector Si and that of the backscattered wave by a Stokes vector Ss, then the backscattered power from a scatterer is defined by
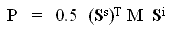(2-5)
where M is the Stokes matrix, which is a 4x4 array of real numbers page 291, . In other words, the Stokes matrix is another way of transforming the incident EM wave into the backscattered wave.
Assuming reciprocity, the Stokes matrix is symmetric, containing 10 different numbers, of which 9 are independent. Each element can be computed from the scattering matrix.
The Mueller matrix is a close relative of the Stokes matrix, except that reciprocity is not assumed and so it contains more independent elements. The Mueller matrix is used in the FSA convention. There is an equivalent form of the power equation (2-5) for the Mueller matrix, and for the covariance and coherency matrices as well.
The Kennaugh matrix K is the version of the Stokes matrix used in the BSA convention. They are related by M = diag[1 1 1 -1] K. The trace of the Kennaugh matrix equals the total power, but the trace of the Mueller matrix does not. The elements of the Kennaugh matrix are defined in .
Remark: Unfortunately, there is inconsistency in the literature about the naming of the matrix M in (2-5). The convention used here comes from page 119 of Raney's chapter in the Manual of Remote Sensing . The matrix M is called the Stokes scattering operator on page 29 of the Ulaby & Elachi book . We assume the conventions used in the Manual of Remote Sensing in this tutorial.
Page details
- Date modified: