Spectral Resolution

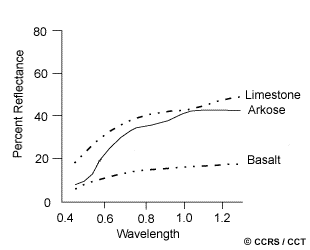
In Chapter 1, we learned about spectral response and spectral emissivity curves which characterize the reflectance and/or emittance of a feature or target over a variety of wavelengths. Different classes of features and details in an image can often be distinguished by comparing their responses over distinct wavelength ranges. Broad classes, such as water and vegetation, can usually be separated using very broad wavelength ranges - the visible and near infrared - as we learned in section 1.5. Other more specific classes, such as different rock types, may not be easily distinguishable using either of these broad wavelength ranges and would require comparison at much finer wavelength ranges to separate them. Thus, we would require a sensor with higher spectral resolution. Spectral resolution describes the ability of a sensor to define fine wavelength intervals. The finer the spectral resolution, the narrower the wavelength range for a particular channel or band.

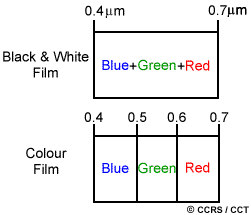
Black and white film records wavelengths extending over much, or all of the visible portion of the electromagnetic spectrum. Its spectral resolution is fairly coarse, as the various wavelengths of the visible spectrum are not individually distinguished and the overall reflectance in the entire visible portion is recorded. Colour film is also sensitive to the reflected energy over the visible portion of the spectrum, but has higher spectral resolution, as it is individually sensitive to the reflected energy at the blue, green, and red wavelengths of the spectrum. Thus, it can represent features of various colours based on their reflectance in each of these distinct wavelength ranges.

Many remote sensing systems record energy over several separate wavelength ranges at various spectral resolutions. These are referred to as multi-spectral sensors and will be described in some detail in following sections. Advanced multi-spectral sensors called hyperspectral sensors, detect hundreds of very narrow spectral bands throughout the visible, near-infrared, and mid-infrared portions of the electromagnetic spectrum. Their very high spectral resolution facilitates fine discrimination between different targets based on their spectral response in each of the narrow bands.

Whiz quiz

1. Hyperspectral scanners (mentioned in Chapter 2.4) are special multispectral sensors which detect and record radiation in several (perhaps hundreds) of very narrow spectral bands. What would be some of the advantages of these types of sensors? What would be some of the disadvantages?
The answer is ...

2. If the spectral range of the 288 channels of the CASI (Compact Airborne Spectrographic Imager) is exactly 0.40 μm to 0.90 μm and each band covers a wavelength of 1.8 nm (nanometres, 10-9 m), will there be any overlap between the bands?
The answer is ...

Whiz quiz - answer

Answer 1: Hyperspectral scanners have very high spectral resolution because of their narrow bandwidths. By measuring radiation over several small wavelength ranges, we are able to effectively build up a continuous spectrum of the radiation detected for each pixel in an image. This allows for fine differentiation between targets based on detailed reflectance and absorption responses which are not detectable using the broad wavelength ranges of conventional multispectral scanners. However, with this increased sensitivity comes significant increases in the volume of data collected. This makes both storage and manipulation of the data, even in a computer environment, much more difficult. Analyzing multiple images at one time or combining them, becomes cumbersome, and trying to identify and explain what each unique response represents in the "real world" is often difficult.

Answer 2: The total wavelength range available will be 0.90-0.40 μm = 0.50 μm. If there are 288 channels of 1.8 nm each, let's calculate the total wavelength range they would span if they did not overlap.

1.8 nm = 1.8 x 10-9 m
1.8 x10-9 m X 288 = 0.0000005184 m
0.0000005184 m = 0.5184 μm

Since 0.5184 is greater than 0.50, the answer is YES, there will be have to be some overlap between some or all of the 288 bands to fit into this 0.50 μm range.